Solving a Maze

Solving a maze is exhilarating. It's not just about finding a way out; it's a test of problem-solving, creativity, and perseverance. Each maze is unique and forces us to think outside the box. What makes this even more interesting is the beautiful graphics that gets generated as the player discovers the path!

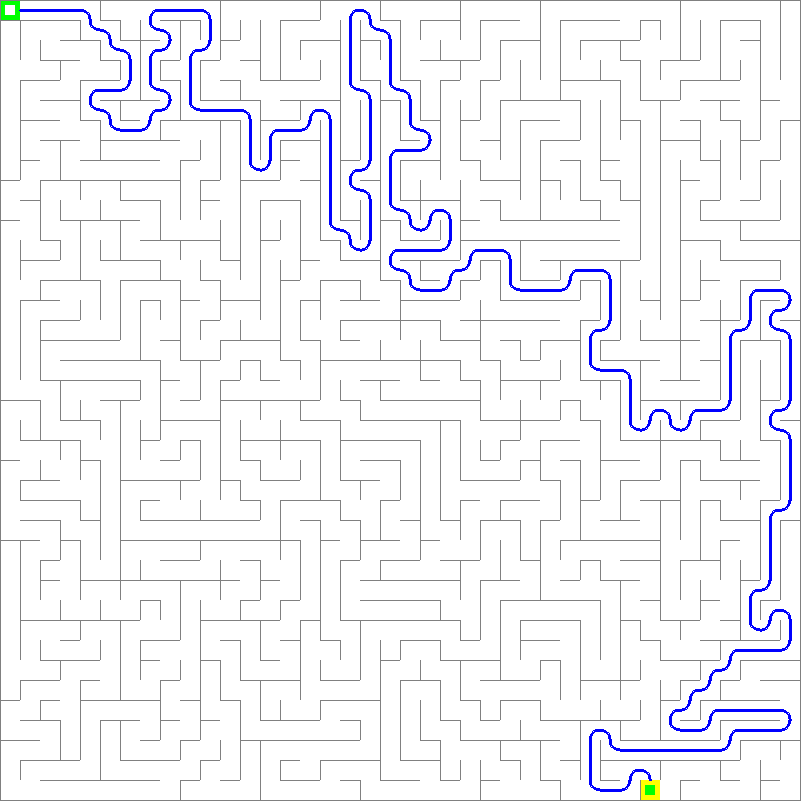
The player automatically navigates through a maze, updating the display to show the current path taken until the exit is reached or the player gets stuck.

Let's break down the key components of the code:

def get_previous_cell_side(previous, p):
    # 0,1,2,3 for top , right , bottom , left
    if previous.y + width == p.y:
        return 0
    elif previous.y == p.y + width:
        return 2
    elif previous.x == p.x + width:
        return 1 # previous is right of p 
    else:
        return 3 # previous left of p

get_previous_cell_side(previous, p) 

• This function determines the relative position of two cells (previous and p) in the maze. It returns an integer representing the side of the previous cell relative to p based on its x and y coordinates

• The return value 0, 1, 2, or 3 corresponds to top, right, bottom, and left, respectively.

def solve_maze(p, previous, stack=0):
    global player, last_traversed_cell
    traversed_path.append(p)
    time.sleep(.02)
    draw_maze(flip=False)
    traversed_path[0].draw(GREEN, False)
    exit_cell.draw(YELLOW, False)
    player.draw(GREEN, True, True)
    draw_path_taken()
    pygame.display.flip()
    
    # print(stack, "Player", p.x//width, p.y//width)  
    if p.get_rect().colliderect(exit_cell.get_rect()):
        return True
    walls_list = [0,1,2,3]
    for i in range(len(p.walls)):
        random_wall = random.choice(walls_list)
        walls_list.remove(random_wall)
        np = None
        if p.walls[random_wall] == False:
            coming_from = get_previous_cell_side(previous,p)
            # print(stack, "coming_from", coming_from)
            # no wall
            if random_wall == 3 and coming_from != 3:
                np = grid[p.y//width][p.x//width - 1] 
            elif random_wall == 1 and coming_from != 1:
                np = grid[p.y//width][p.x//width + 1]
            elif random_wall == 0 and coming_from != 0:
                np = grid[p.y//width - 1][p.x//width]
            elif random_wall == 2 and coming_from != 2:
                np = grid[p.y//width + 1][p.x//width]
            if np is not None:
                # print(stack, "Next Player", np.x//width, np.y//width)  
                player = np
                if solve_maze(player, p, stack + 1):
                    return True
            
    traversed_path.pop()
    gc.collect()
    return False

solve_maze(p, previous, stack=0) 

• Recursive function to solve the maze by moving from one cell (player) to another (np), marking the path taken.

• We visually update the maze's current state, drawing the player's movement, the path taken, and the exit cell.

• We are using backtracking algorithm combined with randomly (random.choice(walls_list)) selecting the next cell, based on the walls of the current cell (p.walls)

• Player iteratively tries to move to adjacent cells (without walls in between) that are not in the direction it came from (coming_from). If a valid move is found, solve_maze is called (recursion) with the new position of the player.

• If the exit is reached, the recursion unwinds, returning True all the way up.

• If no valid moves are found, player backtracks by removing the last cell from traversed_path and returns False.

def auto_play():   
    global player, last_traversed_cell, solved
    done=False
    while not done:
        clock.tick(60)
        for event in pygame.event.get():
            if event.type == pygame.QUIT:
                done = True

        # player
        if not solved:
            if solve_maze(player, player):
                # print("Solved")
                solved=True
                pygame.image.save(screen,"maze_solved.png")
            else:
                print("Got Stuck")

        draw_maze(flip=False)
        traversed_path[0].draw(GREEN, False)
        exit_cell.draw(YELLOW, False)
        player.draw(GREEN, True, True)
        draw_path_taken()
        pygame.display.flip()
        
auto_play()

auto_play() 

• The main game loop -- we keep updating the maze visualization until the maze is solved or the user exits the program

• Call solve_maze with the starting position of the player. If the maze is solved, we save a screenshot of the solved maze and sets solved to True.

This is an interesting application of recursive algorithm and random choice selection to solve a maze puzzle.

Here is the video showing automated path discovery. You can see back propagation in-action!